算法之空间复杂度
空间复杂度(Space Complexity)
空间复杂度的分析方法很少;分析空间复杂度主要从3个点进行分析:
- 算法所占空间
- 算法辅助变量所占内存
- 输入输出数据所占用的空间
注意的是空间复杂度大部分情况都是为O(1),只有在涉及到动态分配的空间以及递归、栈所需的空间时才发生改变
对于算法时间和空间往往是相互影响的;
大部分情况下我们更关注的是时间复杂度,下面就看一个以牺牲空间去换时间的例子;
判断某年是否是闰年,这里一般的做法是去编写一套判断的算法;还可以这么做,创建一个当前年份*2大小的数组,吧这个数组的下标做为年份,下标对应位闰年元素就是1,不是则0;显然第一种算法是比第二个元素少增加一个4000+长度的数组,也就是省了很多空间,第二种比第一种少了一套判断的算法,节省了这个算法运行需要的时间。
往往,当追求一个更好的时间复杂度时,会得到一个差劲的空间复杂度,反之;追求一个更好的空间复杂度,会得到一个更差的时间复杂度;
具体还要看自己的抉择判断惹;
想要更精美的代码,多数情况下是要牺牲时间的;
想要追求更快的速度,则牺牲空间。
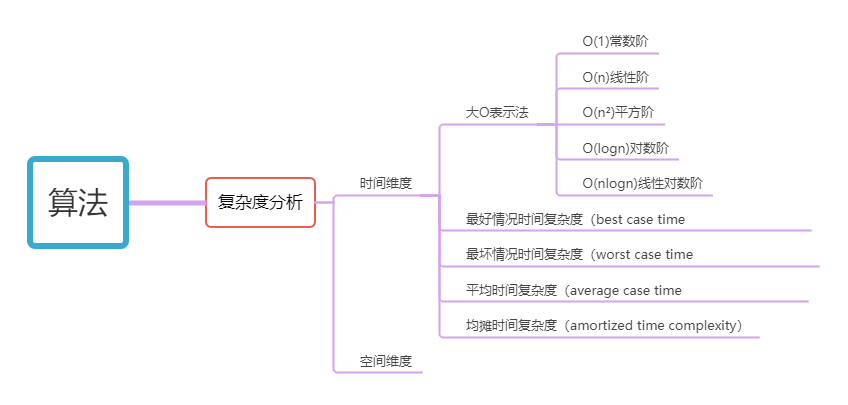
下面关于复杂度的图片分析
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!