算法逻辑之时间概念

时间和空间

算法（Algorithm）是指用来操作数据、解决程序问题的一组方法。

在实际开发中，使用的算法第一时间我们是去考虑其效果和运算时间；不同的算法其运算时间和占用内存是不同的，为了衡量不同算法的优劣和特点，主要从这俩维度进行切入：

1.时间维度 算法计算完成所需要的时间；

2.空间维度 算法计算所需的内存;

如何分析算法的时间复杂度

一看都这个我是想着，时间复杂度不就是运算时间嘛，整个机子一跑不就知道了；

但是我没考虑到，我拿自己的windows笔记本跑和mac跑，所需时间是不同的；

为了正确的判断和分析时间复杂度;

程序员大佬提出了一个分析方法 大o表示法

引入百度百科对大O表示法的解释：

大O表示法：算法的时间复杂度通常用大O符号表述，定义为T[n] = O(f(n))。称函数T(n)以f(n)为界或者称T(n)受限于f(n)。 如果一个问题的规模是n，解这一问题的某一算法所需要的时间为T(n)。T(n)称为这一算法的“时间复杂度”。当输入量n逐渐加大时，时间复杂度的极限情形称为算法的“渐近时间复杂度”。

n 表示数据规模 ，O(f(n))表示运行算法所需要执行的指令数，和f(n)成正比。

大O表示法复杂度量级

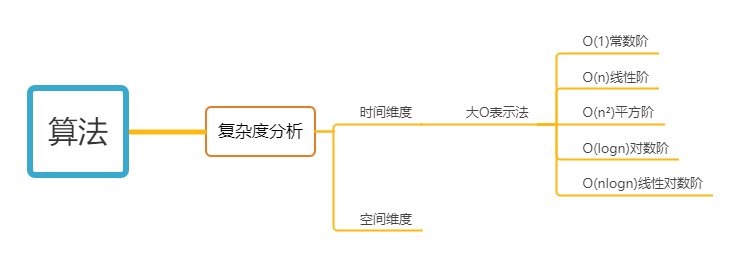
这五个阶级都能用代码体现出来，结合代码还是非常容易理解的。

O(1)常数阶

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/**
    * @Description: O(1) 无论怎么运行，代码时间复杂度都是常量O(1),其他区域的操作不会影响复杂度
    * @Param: * @param
    * @return: void
    * @Author: 虾
    * @Date: 2020/2/1 18:29
    */
    @Test
    public void ConstantOrder(){
            int a=1;
            int b=2;
            int c=a+b;
            int d=c--;
    }

O(n)线性阶

1
2
3
4
5
6
7
8
9
10
11
12
13
/** 
* @Description: O(n) 代码时间复杂度由n的大小而变化呈线性变化就是正比；
* @Param: * @param  
* @return: void 
* @Author: 虾
* @Date: 2020/2/1 18:35
*/
@Test
public void LinearOrder(){
    int n=1;
    for (int i=0;i<n;i++)     
        n=i;        
}

O(n^2)平方阶

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/**
     * @Description: O(n^2) 代码时间复杂度由n的2次方进行增长，再java里面最常见的就是嵌套循环了
     * @Param: * @param
     * @return: void
     * @Author: 虾
     * @Date: 2020/2/1 18:35
     */
    @Test
  public void SquareOrder(){
        int n=1;
        for (int i=0;i<n;i++)
            n=i;
            for (int j=0;j<n;j++)
                n = j;
    }

O(logn)对数阶

这里得提一下对数的基本概念

【定义】如果 N=ax（a>0,a≠1），即a的x次方等于N（a>0，且a≠1），那么数x叫做以a为底N的对数（logarithm），记作：

　　 x=logaN

　　其中，a叫做对数的底数，N叫做真数，x叫做 “以a为底N的对数”。

我也不是特别理解这玩意，头疼。

结合二分法的运作理念好理解一些；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
    * @Description: O(logN) 这里最典型的就是二分查找法 时间复杂度为log3 
    * @Param: * @param
    * @return: int
    * @Author: 虾
    * @Date: 2020/2/1 19:47
    */
    @Test
    public int LogNOrder()
    {
        int[] array ={1,2,3,4,6,7,8,9,10};
        int key=3;
        int left = 0; //第一个下标
        int right = array.length - 1;//最后一个下标
        int current = 0;

        while (left <= right) {
            current = (left + right) / 2;//从中间开始查找
            if (current == key) {
                return array[current];
            } else if (current < key) {
                left = current + 1;
            } else {
                right = current - 1;
            }
        }
        return -1;
    }

O(nlogn)线性对数阶

这个很好理解 就是将时间复杂度为O(logn)的代码循环n遍所需时间。

参考 https://www.cxyxiaowu.com/1996.html