特殊的平衡二叉树：红黑树

前言

算法（Algorithm）是指用来操作数据、解决程序问题的一组方法。

学习这个之前首先要明白平衡二叉树的一些知识

可参考:

https://www.zhbzdnb.com/2019/10/27/mysql%E6%95%B0%E6%8D%AE%E5%BA%93%E7%B4%A2%E5%BC%95%E5%8E%9F%E7%90%86btree%E5%92%8Cb-tree/](https://www.zhbzdnb.com/2019/10/27/mysql数据库索引原理btree和b-tree/)

红黑树和平衡二叉树关系如同b+tree和btree一样；

他们最大的区别在于 所谓平衡；

1、红黑树放弃了追求完全平衡，追求大致平衡，在与平衡二叉树的时间复杂度相差不大的情况下，保证每次插入最多只需要三次旋转就能达到平衡，实现起来也更为简单。

2、平衡二叉树追求绝对平衡，条件比较苛刻，实现起来比较麻烦，每次插入新节点之后需要旋转的次数不能预知。

理解

红黑树是每个节点都带有颜色属性的二叉查找树，颜色或红色或黑色。

红黑树的一些特性：

1. 节点是红色或者黑色
2. 根节点是黑色
3. 每个叶子节点都是黑色的 Nil java中为null
4. 每个红色节点的两个子节点都是黑色的
5. 从任意节点到他的每个叶子的所有路径都包含数量相同i的黑色节点；

下面是一个简单的红黑树

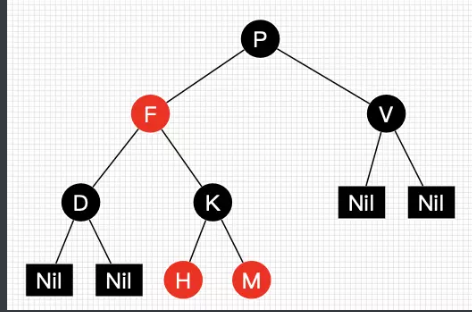
黑色完美平衡概念

可以看出来左子树和右子树层数不相等，但是黑色的层数相等。

这就是黑色完美平衡概念

红黑树自平衡的依据

这里为了便于理解，引入下图，此图取自别人的博客

红黑树自平衡依据： 左旋、右旋和变色。

左旋：以某个结点作为支点(旋转结点)，其右子结点变为旋转结点的父结点，右子结点的左子结点变为旋转结点的右子结点，左子结点保持不变。

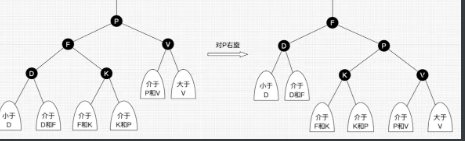
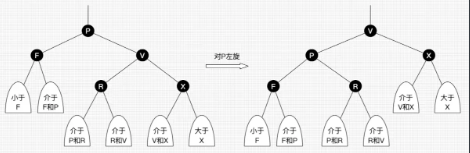右旋：以某个结点作为支点(旋转结点)，其左子结点变为旋转结点的父结点，左子结点的右子结点变为旋转结点的左子结点，右子结点保持不变。如图4。

变色：引入列子

插入一个红色节点时

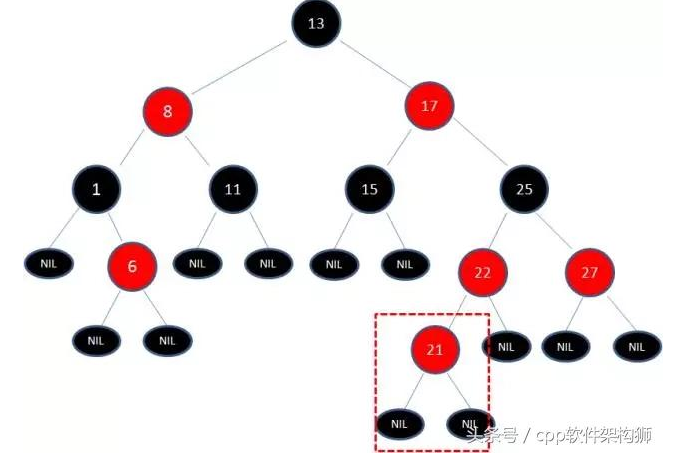
这样显然不符合 :红色节点的两个子节点都是黑色的

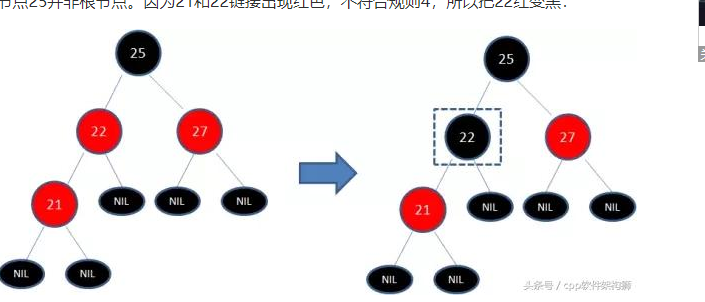
25到21的左叶子经历了一个黑色节点 22 而25到27的叶子没有经历一个黑色子节点

将22弄成黑色；这样不符合:从任意节点到他的每个叶子的所有路径都包含数量相同i的黑色节点；

再次变色 将27变为黑色 满足红黑树5大性质

由此红黑树的一些基本性质和概念完结

参考： http://www.360doc.com/content/18/0904/19/25944647_783893127.shtml

https://www.jianshu.com/p/e136ec79235c