mysql数据库索引原理btree和b+tree

前言

算法（Algorithm）是指用来操作数据、解决程序问题的一组方法。

大家或多或少都知道索引用来提高数据库查询速度，缺点是影响其他非查询的数据库操作速度。

为什么 老子不知道 我就摸摸底层

数据库的底层数据结构多采用b+tree，如innodb

如果数据库底层就一个很普通的键值存储结构

一个很简单的查询 select * from 表 where 主键id=xxx

此表有一亿条数据

那么数据库在这种结构下 是需要执行最多一亿次轮询查询比较

用代码表示if yyy==xxx return

那么就是最多一亿次的磁盘io读取操作 ，这对磁盘的资源占用和查询速度的影响是恐怖的。

梳理

  1. MySQL官方对于索引的定义为：索引是帮助MySQL高效获取数据的数据结构。即：索引是数据结构。

  2. 为了提高查询速度，数据库设计师肯定要从数据库轮询算法的角度进行优化、 最基本的查询算法当然是顺序查找（linear search），这种复杂度为O(n)的算法在数据量很大时显然是糟糕的，好在计算机科学的发展提供了很多更优秀的查找算法，例如二分查找（binary search）、二叉树查找（binary tree search）等。如果稍微分析一下会发现，每种查找算法都只能应用于特定的数据结构之上，例如二分查找要求被检索数据有序，而二叉树查找只能应用于二叉查找树上，但是数据本身的组织结构不可能完全满足各种数据结构（例如，理论上不可能同时将两列都按顺序进行组织），所以，在数据之外，数据库系统还维护着满足特定查找算法的数据结构，这些数据结构以某种方式引用（指向）数据，这样就可以在这些数据结构上实现高级查找算法。这种数据结构，就是索引。

  3. 二叉排数树>二叉平衡树->btree->b+tree

二叉排序树

可以吧这个树看作是btree的前身；

  • 若左子树不空，则左子树上所有节点的值均小于它的根节点的值

  • 若右子树不空，则右字数上所有节点的值均大于它的根节点的值

  • 它的左、右子树也分别为二叉排序数（递归定义）

  • 1572187116985

    img

二叉排序树组织数据时，用于查找是比较方便的，因为每次经过一次节点时，最多可以减少一半的可能，不过极端情况会出现所有节点都位于同一侧，直观上看就是一条直线，那么这种查询的效率就比较低了，需要多次查找；因此需要对二叉树左右子树的高度进行平衡化处理，于是就有了平衡二叉树（Balenced Binary Tree）。

平衡二叉树（AVL Tree）

平衡二叉树（AVL树）在符合二叉查找树的条件下，还满足任何节点的两个子树的高度最大差为1。 左边是AVL树，它的任何节点的两个子树的高度差<=1；右边的不是AVL树，其根节点的左子树高度为3，而右子树高度为1；

img

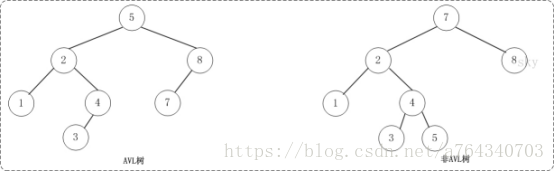
但是要对树进行插入或删除的操作会打破平衡，可通过旋转让平衡树恢复平衡

这里不深入去学习了，有兴趣这里查看

https://blog.csdn.net/a764340703/article/details/82621781

平衡多路查找树（B-Tree）

一棵m阶的B-Tree有如下特性：

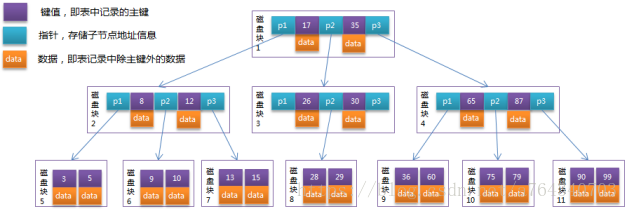
​ m代表阶级 下面图片就是一个三阶的btree

  1. 每个节点最多有m个孩子。
  2. 除了根节点和叶子节点外，其它每个节点至少有Ceil(m/2)个孩子。
  3. 若根节点不是叶子节点，则至少有2个孩子
  4. 所有叶子节点都在同一层，且不包含其它关键字信息
  5. 每个非终端节点包含n个关键字信息（P0,P1,…Pn, k1,…kn）
  6. 关键字的个数n满足：ceil(m/2)-1 <= n <= m-1
  7. ki(i=1,…n)为关键字，且关键字升序排序。
  8. Pi(i=1,…n)为指向子树根节点的指针。P(i-1)指向的子树的所有节点关键字均小于ki，但都大于k(i-1)
    借参考博客的一张图 和一段话 我觉得画的很易理解了img

总结归纳一下

B-Tree结构的数据可以让系统高效的找到数据所在的磁盘块。为了描述B-Tree，首先定义一条记录为一个二元组[key, data] ，key为记录的键值，对应表中的主键值，data为一行记录中除主键外的数据。对于不同的记录，key值互不相同。

最下面一层是叶子节点

这个图的三阶 第二层即表示小于第一层的范畴、处于第一层范畴之内、大于第一范畴；对比平衡二叉树多了一个范畴；

注意这里btree每个节点都包含了键值和数据

这里btree根据每个节点最多有m个孩子。平衡二叉树孩子最多俩个；而btree最多可有m个；进而相比平衡二叉树缩减了节点，从而就缩减io读取次数，也就是btree的最终目的；

B+Tree

b+tree就是btree的加强版，他继承了btree的优点；

他俩的主要区别

  1. 非叶子节点只存储键值信息。
  2. 所有叶子节点之间都有一个链指针。
  3. 数据记录都存放在叶子节点中。

主要一点数据记录都在叶子节点中；引用这句话

1
B-Tree结构图中可以看到每个节点中不仅包含数据的key值，还有data值。而每一个页的存储空间是有限的，如果data数据较大时将会导致每个节点（即一个页）能存储的key的数量很小，当存储的数据量很大时同样会导致B-Tree的深度较大，增大查询时的磁盘I/O次数，进而影响查询效率。在B+Tree中，所有数据记录节点都是按照键值大小顺序存放在同一层的叶子节点上，而非叶子节点上只存储key值信息，这样可以大大加大每个节点存储的key值数量，降低B+Tree的高度。

参考： https://blog.csdn.net/a764340703/article/details/82621781